Оптимальное управление зависит от модели управляемой системы. Теория оптимального управления. Критерий оптимального управления производственных систем

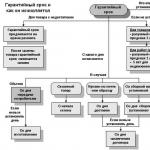
В общем случае автоматическая система состоит из объекта управления и совокупности устройств, которые обеспечивают управление этим объектом. Как правило, эта совокупность устройств включает в себя измерительные устройства, усилительные и преобразовательные устройства, а также исполнительные устройства. Если объединить эти устройство в одно звено (управляющее устройство), то структурная схема системы выглядит следующим образом:

В автоматической системе информация о состоянии объекта управления через измерительное устройство поступает на вход управляющего устройства. Такие системы называются системами с обратной связью или замкнутыми системами. Отсутствие этой информации в алгоритме управления говорит о том, что система разомкнута. Состояние объекта управления в любой момент времени будем описывать переменными
, которые называются координатами системы или переменными состояния. Их удобно считать координатами- мерного вектора состояния.

Измерительное устройство выдает информацию о состоянии объекта. Если на основании измерения вектора
могут быть найдены значения всех координат
вектора состояния
, то говорят, что система полностью наблюдаема.

Управляющее устройство вырабатывает управляющее воздействие
. Таких управляющих воздействий может быть несколько, они образуют- мерный управляющий вектор.

На вход управляющего устройства поступает задающее входное воздействие
. Это входное воздействие несет информацию о том, какое должно быть состояние объекта. На объект управления может действовать возмущающее воздействие
, которое представляет собой нагрузку или помеху. Измерение координаты объекта, как правило, осуществляется с некоторыми погрешностями
, которые тоже носят случайный характер.

Задачей управляющего устройства является выработка такого управляющего воздействия
, чтобы качество функционирования автоматической системы в целом было бы наилучшим в некотором смысле.

Мы будем рассматривать такие объекты управления, которые являются управляемыми. То есть вектор состояния можно изменять требуемым образом путем соответствующего изменения вектора управления. Будем подразумевать, что объект полностью наблюдаемый.

Так, например, положение летательного аппарата характеризуется шестью координатами состояния. Это
- координаты центра масс,
- углы Эйлера, определяющие ориентацию летательного аппарата относительно центра масс. Положение летательного аппарата можно изменить с помощью рулей высоты, курса, элерона и с помощью уклонения вектора силы тяги. Таким образом управляющий вектор определен следующим образом:

- угол отклонения рулей высоты

- курс

- элерон

- тяга

Вектор состояния
в этом случае определяется следующим образом:

Можно поставить задачу выбора управления, с помощью которого летательный аппарат переводится из заданного начального состояния
в заданное конечное состояние
с минимальными затратами топлива или за минимальное время.

Дополнительная сложность при решении технических задач возникает в силу того, что на управляющее воздействие и на координаты состояния объекта управления, как правило, накладываются различные ограничения.

На любой угол рулей высоты, курса, элерона существуют ограничения:

- тяга сама по себе ограничена.

На координаты состояния объекта управления и их производные также накладываются ограничения, которые связаны с допустимыми перегрузками.

Мы будем рассматривать объекты управления, которые описываются дифференциальным уравнением:

(1)

Или в векторном виде:

--мерный вектор состояния объекта

--мерный вектор управляющих воздействий

- функция правой части уравнения (1)

На вектор управления
накладывается ограничение, мы будем полагать, что его значения принадлежат некоторой замкнутой областинекоторого-мерного пространства. Это означает, что управляющая функция
в любой момент времени принадлежит области(
).

Так, например, если координаты управляющей функции удовлетворяет неравенствам:

то область является-мерным кубом.

Назовем допустимым управлением всякую кусочно-непрерывную функцию
, значения которой в каждый момент временипринадлежит области, и которая может иметь разрывы первого рода. Оказывается, даже в некоторых задачах оптимального управления решение может быть получено в классе кусочно-непрерывного управления. Для того, чтобы выбрать управление
как функцию времени и начального состояния системы
, которое однозначно определяет движение объекта управления, требуется, чтобы система уравнений (1) удовлетворяла условиям теоремы существования и единственности решения в области
. В этой области располагаются возможные траектории движения объекта и возможные управляющие функции
. Если область изменения переменных является выпуклой, то для существования и единственности решения достаточно, чтобы функции

. были непрерывны по всем аргументам и имели непрерывные частные производные по переменным

.

В качестве критерия, который характеризует качество работы системы, выбирается функционал вида:

(2)

В качестве функции
будем предполагать, что она непрерывна по всем своим аргументам и имеет непрерывные частные производные по

.

Государственное образовательное учреждение

высшего профессионального образования

Московский физико-технический институт

(государственный университет)

УТВЕРЖДАЮ

Проректор по учебной работе

Ю.А.Самарский

«____»_______________2004 г.

П Р О Г Р А М М А

по курсу: ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ

по направлению 511600

факультет ФУПМ

кафедра математических основ управления

курс IV

семестр 7, 8

лекции – 50 час. Экзамен – 8 семестр

семинары – 50 час. Зачет – 7 семестр

лабораторные занятия – нет

Самостоятельная работа – 2 часа в неделю

ВСЕГО ЧАСОВ 100

Программу и задание составил: д.ф.-м.н., профессор Жадан В.Г.

Заведующий кафедрой С.А. Гуз

1. Основная задача оптимального управления. Принцип максимума Л.С. Понтрягина (принцип минимума). Каноническая форма записи. Принцип максимума для систем, содержащих управляющие параметры.

2. Задачи с подвижным правым концом. Условия трансверсальности. Задачи Лагранжа и Больца. Задачи Майера и Лагранжа с нефиксированным временем окончания процесса. Задача на быстродействие. Задача с подвижным левым концом.

3. Доказательство принципа максимума Л.С. Понтрягина для задачи Майера. Понятие игольчатой вариации. ЛеммаГронуолла–Беллмана. Учет оптимизации по управляющему параметру.

4. Связь принципа максимума с вариационным исчислением. Уравнение Эйлера. Первые интегралы уравнения Эйлера. Условия Веерштрасса, Лежандра и Якоби. Уравнение Якоби. Условия Веерштрасса–Эрдмана.

5. Линейные системы. Принцип максимума для линейных систем. Теорема о конечном числе точек переключений.

6. Множество достижимости для линейных систем. Экстремальное управление и экстремальный принцип.

7. Точечная управляемость для линейных систем. Критерий точечной управляемости. Теорема Калмана о точечной управляемости. Полная управляемость линейных систем. Теорема Калмана о полной управляемости автономных систем.

8. Проблема наблюдаемости. Критерий наблюдаемости для линейной системы. Наблюдение начального состояния. Связь между наблюдаемостью и управляемостью. Критерий полной наблюдаемости стационарной системы.

9. Формализм Лагранжа и его использование для решения задач оптимального управления. Проблема синтеза оптимального управления.

10. Проблема идентификации. Критерий идентифицируемости. Критерий полной идентифицируемости стационарной системы.

11. Системы с разрывными правыми частями. Условие скачка импульсов.

12. Понятие инвариантных систем. Свойства динамических систем. Опорное поле импульсов. Необходимые и достаточные условия инвариантности. Корректирующая функция.

13. Достаточные условия оптимальности. Поле экстремалей. Связь с достаточными условиями Веерштрасса для классической задачи вариационного исчисления.

14. Элементы теории динамического программирования. Необходимые условия оптимальности. Достаточные условия оптимальности. Уравнение Беллмана. Вывод принципа максимума из динамического программирования. Связь с вариационным исчислением.

15. Методы решения краевых задач. Применение метода Ньютона. Перенос граничных условий. Метод прогонки для нелинейных задач.

16. Численные методы, основанные на последовательном анализе вариантов. Метод «киевского веника», метод блуждающей трубки, метод локальных вариаций.

17. Численные методы, основанные на редукции к задачам нелинейного программирования. Вычисление производных по компонентам вектора управлений в случае дискретных процессов. Метод штрафов, метод нагруженного функционала.

18. Дискретный принцип минимума. Вариационные неравенства. Применение метода условного градиента для решения задач оптимального управления. Принцип квазиминимума.

19. Достаточные условия оптимальности В.Ф. Кротова для непрерывных и дискретных процессов. Применение формализма В.Ф. Кротова для решения линейных задач.

20. Особые управления. Определение особых управлений с помощью скобок Пуассона. Условия Келли и Коппа–Мойера.

СПИСОК ЛИТЕРАТУРЫ

1. Моисеев Н.Н. Численные методы в теории оптимальных систем. – М.: Наука, 1971.

2. Евтушенко Ю.Г. Методы решения экстремальных задач и их применение в системах оптимизации. – М.: Наука, 1982.

3. Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации. – М.: Наука, 1987.

4. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе З.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. – М.: Физматгиз, 1961.

5. Васильев Ф.П. Методы решения экстремальных задач. – М.: Наука, 1988.

6. Габасов Р., Кириллова Ф.М. Принцип максимума в теории оптимального управления. – Минск: Наука и техника, 1974.

7. Флеминг У., Ришел Р. Оптимальное управление детерминированными и стохастическими системами. – М.: Мир, 1978.

8. Основы теории оптимального управления /Под редакцией В.Ф. Кротова. – М.: Высшая школа, 1990.

9. Ли Э.Б., Маркус П. Основы теории оптимального управления. М.: Наука, 1972.

10. ГабасовР., Кириллова Ф.М. Особые оптимальные управления. – М.: Наука, 1973.

Задание можно посмотреть

Оптимальное управление технологическими процессами (Лекция)

ПЛАН ЛЕКЦИИ

1. Основные понятия нахождения экстремума функции

2. Классификация методов оптимального управления

1. Основные понятия нахождения экстремума функции

Всякая математическая постановка оптимальной задачи часто равносильна или эквивалентна задаче отыскания экстремума функции одной или многих независимых переменных. Поэтому для решения таких оптимальных задач могут быть использованы различные методы поиска экстремума.

В общем случае задача оптимизации формулируется следующим образом:

Найти extr функции R (x ), где ХХ

R (x ) – называется целевой функцией или функцией или критерием оптимизации или оптимизируемой функцией

Х – независимая переменная.

Как известно необходимые условиям существования экстремума у непрерывной функции R (x ) могут быть получены из анализа первой производной . При этом функция R (x ) может иметь экстремальные значения при таких значениях независимой переменной Х, где первая производная равна 0. т.е. =0. Графически равенство нулю производной означает, что касательная к кривой R (x ) в этой точке параллельна оси абсцисс.

Равенство производной =0 есть необходимое условие экстремума.

Однако равенство нулю производной еще не означает, что в этой точке существует экстремум. Для того, чтобы окончательно убедится, что в этой точке действительно существует экстремум необходимо провести дополнительные исследования, которые заключаются в следующих способах:

1. Способ сравнения значений функций

Сравнивают значение функции R (x ) в «подозреваемой» на экстремум точке Х К две соседние значения функции R (x ) в точках Х К-ε и Х К+ε , где ε- малая положительная величина. (Рис. 2)

Если оба рассчитанных значения R (Х К+ε) и R (Х К-ε), окажутся меньше или больше R (Х К), то в точке Х К существует максимум или минимум функции R (х).

Если же R (Х К) имеет промежуточное значение между R (Х К-ε) и R (Х К+ε), то функция R (х) не имеет ни максимума ни минимума.

2. Способ сравнения знаков производных

Опять рассмотрим функцию R (Х К) в окрестностях точки Х К, т.е. Х К+ε и Х К-ε . При этом способе рассматривается знак производной в окрестности точки Х К. Если знаки производной в точках Х К-ε и Х К+ε различные, то в точке Х К существует экстремум. При этом вид экстремума (min или max ) может быть найден по изменению знака производной при переходе от точки Х К-ε к точке Х К+ε.

Если знак меняется с «+» на «-», то в точке Х К – максимум (рис. 3б), если наоборот с «-» на «+», то минимум. (Рис. 3а)

3. Способ исследования знаков высших производных.

Этот способ применяют в тех случаях, когда в точке «подозреваемой» на экстремум существуют производные высших порядков, т.е. функция R (Х К) не только сама непрерывна, но имеет также непрерывные производные и .

Способ сводится к следующему:

В точке Х К «подозреваемой» на экстремум, для которой справедливо

вычисляется значение второй производной .

Если при этом , то в точке Х К – максимум,

если , то в точке Х К – минимум.

При решении практических задач оптимизации требуется отыскать не какое-нибудь min или max значение функции R (Х К), а наибольшее или наименьшее значение этой функции, которое называется глобальным экстремумом. (Рис. 4)

В общем случае задача оптимизации состоит в отыскивании экстремума функции R (Х), при наличии тех или иных ограничений на уравнения математической модели.

В том случае, если R (Х) является линейной, а область допустимых решений задается линейными равенствами и неравенствами, то задача отыскания экстремумов функции относится к классу задач линейного программирования.

Часто множество Х определяют как систему функции

Тогда запись математической постановки задачи линейного программирования выглядит так:

В том случае, если или целевая функция R (Х) или какая-либо из ограничений не является линейной функцией, то задача отыскания экстремума функции R (Х) относится к классу задач нелинейного программирования.

В том случае, если на переменные Х не наложено никаких ограничений, то такая задача называется задачей на безусловный экстремум.

Пример типовой задачи оптимизации

Задача о коробке максимального объема.

Из этой заготовки следует вырезать четыре ровных квадрата по ее углам, а полученную фигуру (рис.5 б) согнуть так, чтобы получилась коробка без верхней крышки (рис.6.5 в). при этом необходимо так выбрать размер вырезаемых квадратов, чтобы получилась коробка максимального объема.

На примере данной задачи можно проиллюстрировать все элементы постановки задач оптимизации.

Рис. 5. Схема изготовления коробки из прямоугольной заготовки фиксированного размера

Оценочной функцией в данной задаче служит объем изготовленной коробки. Проблема заключается в выборе размера вырезаемых квадратов. Действительно, если размер вырезаемых квадратов слишком мал, то будет получена широкая коробка малой высоты, а значит и объем окажется невелик. С другой стороны, если размер вырезаемых квадратов будет слишком большой, то будет получена узкая коробка большой высоты, а значит, и ее объем также окажется невелик.

В то же время на выбор размера вырезаемых квадратов оказывает влияние ограничение размера исходной заготовки. Действительно, если вырезать квадраты со стороной, равной половине стороны исходной заготовки, то задача теряет смысл. Сторона вырезаемых квадратов также не может превышать половину сторон исходной заготовки, поскольку это невозможно из практических соображений. Из этого следует, что в постановке данной задачи должны присутствовать некоторые ограничения.

Математическая постановка задачи о коробке максимального объема . Для математической постановки данной задачи необходимо ввести в рассмотрение некоторые параметры, характеризующие геометрические размеры коробки. С этой целью дополним содержательную постановку задачи соответствующими параметрами. С этой целью будем рассматривать квадратную заготовку из некоторого гибкого материала, которая имеет длину стороны L (рис. 6). Из этой заготовки следует вырезать четыре ровных квадрата со стороной по ее углам, а полученную фигуру согнуть, так чтобы получилась коробка без верхней крышки. Задача состоит в таком выборе размера вырезаемых квадратов, чтобы в результате получилась коробка максимального объема.

Рис. 6. Схема изготовления из прямоугольной заготовки с указанием ее размеров

Для математической постановки данной задачи необходимо определить переменные соответствующей задачи оптимизации, задать целевую функцию и специфицировать ограничения. В качестве переменной следует взять длину стороны вырезаемого квадрата r , которая в общем случае, исходя из содержательной постановки задачи, принимает непрерывные действительные значения. Целевой функцией является объем полученной коробки. Поскольку длина стороны основания коробки равна: L - 2r , а высота коробки равна r , то ее объем находится по формуле: V (r) = (L -2r ) 2 r . исходя из физических соображений, значения переменной r не могут быть отрицательными и превышать величину половины размера исходной заготовки L , т.е. 0,5L .

При значениях r = 0 и r = 0,5 L соответствующие решения задачи о коробке являются выраженными. Действительно, в первом случае заготовка остается без изменения, а во втором случае она разрезается на 4 одинаковых части. Поскольку эти решения имеют физическую интерпретацию, задачу о коробке для удобства ее постановки и анализа можно считать оптимизации с ограничениями типа нестрогих неравенств.

С целью унификации, обозначим переменную через х = r , что не оказывает влияния на характер решаемой задачи оптимизации. Тогда математическая постановка задачи о коробке максимального объема может быть записана в следующем виде:

где (1)

Целевая функция данной задачи является нелинейной, поэтому задача о коробке максимального размера относится к классу задач нелинейного программирования или нелинейной оптимизации.

2. Классификация методов оптимального управления

Оптимизация процесса заключается в нахождении оптимума рассматриваемой функции или оптимальных условий проведения данного процесса.

Для оценки оптимума, прежде всего, необходимо выбрать критерий оптимизации. Обычно, критерий оптимизации выбирает из конкретных условий. Это могут быть технологический критерий (например, содержание Сu в отвальном шлаке) или экономический критерий (минимальная стоимость продукта при заданной производительности труда) и др. На основании выбранного критерия оптимизации составляется целевая функция, представляющая собой зависимость критерия оптимизации от параметров влияющих на его значение. Задача оптимизации сводится к нахождению экстремума целевой функции. В зависимости от характера рассматриваемых математических моделей принимаются различные математические методы оптимизации.

Общая постановка задачи оптимизации заключается в следующем:

1. Выбирается критерий

2. Составляется уравнение модели

3. Накладывается система ограничения

4. Решение

модель - линейная или нелинейная

Ограничения

В зависимости от структуры модели применяются различные методы оптимизации. К ним относятся:

1. Аналитические методы оптимизации (аналитический поиск экстремума, метод множителей Лагранжа, Вариационные методы)

2. Математическое программирование (линейное программирование, динамическое программирование)

3. Градиентные методы.

4. Статистические методы (Регрессионный анализ)

Линейное программирование . В задачах линейного программирования критерий оптимальности представляется в виде:

где - заданные постоянные коэффициенты; Переменные задачи.

Уравнения модели представляют собой линейные уравнения (полиномы) вида на которые накладывается ограничения в виде равенства или неравенства, т.е. (2)

В задачах линейного программирования обычно предполагается, что все независимые переменные Х j неотрицательны, т.е.

Оптимальным решением задачи линейного программирования является такая совокупность неотрицательных значений независимых переменных

Которая удовлетворяет условия (2) и обеспечивает в зависимости от постановки задачи max или min значение критерия.

Геометрическая интерпретация имеет вид: - критерий при наличии ограничении на переменных Х 1 и Х 2 типа равенств и неравенств

R имеет постоянное значение вдоль линии l . Оптимальное решение будет в точке S , т.к. в этой точке критерий будет max .Одним из методов решения задачи оптимизации линейного программирования является симплекс-метод.

Нелинейное программирование . Математическая постановка задачи нелинейного программирования заключается в следующем: Найти экстремум целевой функции , которая имеет вид нелинейности.

На независимые переменные налагаются различные ограничения типа равенств или неравенств

в настоящее время для решения задач нелинейного программирования применяются довольно большое число методов.

К ним относится: 1) Градиентные методы (метод градиента, метод наискорейшего спуска, метод образов, метод Розенброка и т.д.)

2) Безградиентные методы (метод Гауса-Зейделя, метод сканирования).

Градиентные методы оптимизации

Эти методы относятся к численным методам поискового типа. Сущность этих методов заключается в определении значений независимых переменных, дающих наибольшее (наименьшее) изменение целевых функции. Обычно это достигается при движении вдоль градиента, ортогонального к контурной поверхности в данной точке.

Рассмотрим метод градиента. В этом методе используется градиент целевой функции. В методе градиента шаги совершаются в направлении наибыстрейшего уменьшения целевой функции.

Рис. 8. Поиск минимума методом градиента

Поиск оптимума производится в два этапа:

1-этап: - находят значения частных производных по всем независимым переменным, которые определяют направление градиента в рассматриваемой точке.

2-этап: - осуществляется шаг в направлении обратном направлению градиента, т.е. в направлении наибыстрейшего убывания целевой функции.

Алгоритм градиентного метода может быть записан следующим образом:

(3)

Характер движения к оптимуму методом наискорейшего спуска заключается в следующем (рис. 6.9), после того как в начальной точке найден градиент оптимизируемой функции и тем самым определено направление ее наибыстрейшего убывания в указанной точке, в данном направлении делается шаг спуска. Если значение функции в результате этого шага уменьшилась, то производится очередной шаг в том же направлении, и так до тех пор, пока в этом направлении не будет найден минимум, после чего вычисляется снова градиент и определяется новое направление наибыстрейшего убывания целевой функции.

Безградиентные методы поиска экстремума. Эти методы, в отличии от градиентных, используют в процессе поиска информации, получаемую не при анализе производных, а от сравнительной оценки величины критерия оптимальности в результате выполнения очередного шага.

К безградиентным методам поиска экстремума относится:

1. метод золотого сечения

2. метод с использованием чисел Фибония

3. метод Гауса-Зейделя (метод получения изменения переменной)

4. метод сканирования и т.д.

Оптимальное управление в последние годы начали применять как в технических системах для повышения эффективности производственных процессов, так и в системах организационного управления для совершенствования деятельности предприятий, организаций, отраслей народного хозяйства.

В организационных системах обычно интересуются конечным, установившимся результатом команды, не исследуя

эффективность во время переходного процесса между отдачей команды и получением окончательного результата Объясняется это тем, что обычно в таких системах потери в переходном процессе достаточно малы и влияют несущественно на общую величину выигрыша в установившемся режиме, поскольку сам установившийся режим значительно более длителен, чем переходный процесс. Но иногда динамика не исследуется из-за математических трудностей. Методам оптимизации конечных состояний в организационных и экономических системах посвящены курсы методов. оптимизации и исследования операций.

В управлении динамическими техническими системами оптимизация часто существенна именно для переходных процессов, в которых показатель эффективности зависит не только от текущих значений координат (как в экстремальном управлении), но и от характера изменения в прошлом, настоящем и будущем, и выражается некоторым функционалом от координат, их производных и, может быть, времени.

В качестве примера можно привести управление бегом спортсмена на дистанции. Так как его запас энергии ограничен физиологическими факторами, а расходование запаса зависит от характера бега, спортсмен уже не может в каждый момент отдавать максимум возможной мощности, чтобы не израсходовать запас энергии преждевременно и не выдохнуться на дистанции, а должен искать оптимальный для своих особенностей режим бега.

Нахождение оптимального управления в подобных динамических задачах требует решения в процессе управления достаточно сложной математической задачи методами вариационного исчисления или математического программирования в зависимости от вида математического описания (математической модели) системы. Таким образом, органической составной частью системы оптимального управления становится счетно-решающее устройство или вычислительная машина. Принцип поясняется на рис. 1.10. На вход вычислительного устройства (машины) ВМ поступает информация о текущих значениях координат х с выхода объекта О, об управлениях и с его входа, о внешних воздействиях z на объект, а также задание извне различных условий: значение критерия оптимальности граничных условий информация о допустимых значениях Вычислительное

Определение и необходимость построения оптимальных систем автоматического управления

Системы автоматического управления обычно проектируют, исходя из требований обеспечения тех или иных показателей качества. Во многих случаях необходимое повышение динамической точности и улучшение переходных процессов систем автоматического управления достигается с помощью корректирующих устройств.

Особенно широкие возможности повышения показателей качества дает введение в САУ разомкнутых компенсационных каналов и дифференциальных связей, синтезированных из того или иного условия инвариантности ошибки относительно задающего или возмущающих воздействий . Однако эффект влияния корректирующих устройств, разомкнутых компенсационных каналов и эквивалентных им дифференциальных связей на показатели качества САУ зависит от уровня ограничения сигналов нелинейными элементами системы. Выходные сигналы дифференцирующих устройств, обычно кратковременные по длительности и значительные по амплитуде, ограничиваются элементами системы и не приводят к улучшению показателей качества системы, в частности ее быстродействия. Лучшие результаты решения задачи повышения показателей качества САУ при наличии ограничений сигнала дает так называемое оптимальное управление.

Задача синтеза оптимальных систем строго сформулирована сравнительно недавно, когда было дано определение понятия критерия оптимальности. В качестве критерия оптимальности в зависимости от цели управления могут быть выбраны различные технические или экономические показатели управляемого процесса. В оптимальных системах обеспечивается не просто некоторое повышение того или иного технико-экономического показателя качества, а достижение минимально или максимально возможного его значения.

Если критерий оптимальности выражает технико-экономические потери (ошибки системы, время переходного процесса, расход энергии, средств, стоимость и т. п), то оптимальным будет такое управление, которое обеспечивает минимум критерия оптимальности. Если Же он выражает рентабельность (к. п. д., производительность, прибыль, дальность полета ракеты и т. д.), то оптимальное управление должно обеспечить максимум критерия оптимальности.

Задача определения оптимальной САУ, в частности синтез оптимальных параметров системы при поступлении на ее вход задающего

воздействия и помехи, являющихся стационарными случайными сигналами, рассматривалась в гл. 7. Напомним, что в данном случае в качестве критерия оптимальности принято среднеквадратическое значение ошибки (СКО). Условия повышения точности воспроизведения полезного сигнала (задающего воздействия) и подавления помехи носят противоречивый характер, и поэтому возникает задача выбора таких (оптимальных) параметров системы, при которых СКО принимает наименьшее значение.

Синтез оптимальной системы при среднеквадратическом критерии оптимальности является частной задачей. Общие методы синтеза оптимальных систем основываются на вариационном исчислении. Однако классические методы вариационного исчисления для решения современных практических задач, требующих учета ограничений, во многих случаях оказываются непригодными. Наиболее удобными методами синтеза оптимальных систем автоматического управления являются метод динамического программирования Беллмана и принцип максимума Понтрягина.

Таким образом, наряду с проблемой улучшения различных показателей качества САУ возникает задача построения оптимальных систем, в которых достигается экстремальное значение того или иного технико-экономического показателя качества.

Разработка и внедрение оптимальных систем автоматического управления способствует повышению эффективности использования производственных агрегатов, увеличению производительности труда, улучшению качества продукции, экономии электроэнергии, топлива, сырья и т.

Понятия о фазовом состоянии и фазовой траектории объекта

В технике часто возникает задача перевода управляемого объекта (процесса) из одного состояния в другое. Например, при целеуказании необходимо антенну радиолокационной станции повернуть из начального положения с начальным азимутом в заданное положение с азимутом Для этого на электродвигатель, связанный с антенной через редуктор, подают управляющее напряжение и. В каждый момент времени состояние антенны характеризуется текущим значением угла поворота и угловой скоростью Эти две величины изменяются в зависимости от управляющего напряжения и. Таким образом, существуют три связанных между собой параметра и (рис. 11.1).

Величины характеризующие состояние антенны, называются фазовыми координатами, и - управляющим воздействием. При целеуказании РЛС типа станции орудийной наводки возникает задача поворота антенны по азимуту и углу места. В этом случае будем иметь четыре фазовые координаты объекта и два управляющих воздействия. У летящего самолета можно рассматривать шесть фазовых координат (три пространственные координаты и три компоненты скорости ) и несколько управляющих воздействий (тяга двигателя, величины, характеризующие положение рулей

Рис. 11.1. Схема объекта с одним, управляющим воздействием и двумя фазовыми координатами.

Рис. 11.2. Схема объекта с управляющими воздействиями и фазовыми координатами.

Рис. 11.3. Схема объекта с векторным изображением управляющего воздействия и и фазового состояния объекта

высоты и направления, элеронов). В общем случае в каждый момент времени состояние объекта характеризуется фазовыми координатами а к объекту может быть приложено управляющих воздействий (рис. 11.2).

Под переводом управляемого объекта (процесса) из одного состояния в другое следует понимать не только механическое перемещение (например, антенны РЛС, самолета), но также требуемое изменение различных физических величин: температуры, давления, влажности кабины, химического состава того или иного сырья при соответствующем управляемом технологическом процессе.

Управляющие воздействия удобно считать координатами некоторого вектора называемого вектором управляющего воздействия. Фазовые координаты (переменные состояния) объекта также можно рассматривать, как координаты некоторого вектора или точки в -мерном пространстве с координатами Эту точку называют фазовым состоянием (вектором состояния) объекта, а -мерное пространство, в котором в виде точек изображаются фазовые состояния, называется фазовым пространством (пространством состояний) рассматриваемого объекта. При использовании векторных изображений управляемый объект можно изобразить, как показано на рис. 11.3, где и - вектор управляющего воздействия и представляет собой точку в фазовом пространстве, характеризующую фазовое состояние объекта. Под влиянием управляющего воздействия и фазовая точка перемещается, описывая в фазовом пространстве некоторую линию, называемую фазовой траекторией рассматриваемого движения объекта.