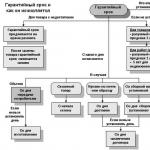
Моделирование свободного движения автомобилей по двухполосным автомобильным дорогам. Моделирование движения самобалансирующегося велосипеда Информатика моделирование движения дискретизация практика
Допустим, вы двигаетесь на велосипеде, и вдруг кто-то толкает вас сбоку. Чтобы быстро восстановить равновесие и избежать падения, вы повернете руль велосипеда в направлении толчка. Велосипедисты делают это рефлекторно, но удивительно, что велосипед может выполнить это действие самостоятельно. Современные велосипеды могут самостоятельно удерживать равновесие даже при движении без управления. Посмотрим, как этот эффект можно смоделировать в COMSOL Multiphysics.
Что мы знаем о самобалансировании велосипедов
Современный велосипед не очень сильно отличается от безопасного велосипеда — одной из первых конструкций, появившейся в 80-х годах XIX века. По прошествии более ста лет ученые все еще пытаются выяснить, за счет каких эффектов велосипед становится самобалансируемым. Другими словами, как неуправлемый велосипед сохраняет равновесие в вертикальном положении? Описанию движения велосипеда с помощью аналитических уравнений посвящено множество опубликованных работ. Одной из первых важных публикаций по этой теме была статья Фрэнсиса Уиппла, в которой он получил общие нелинейные уравнения динамики велосипеда, управляемого велосипедистом без использования рук.
Принято считать, что устойчивость велосипеда обеспечивается двумя факторами — гироскопической прецессией переднего колеса и стабилизирующим действием продольного наклона оси поворота колеса. Совсем недавно команда исследователей из Делфта и Корнелла (см. ) опубликовала всеобъемлющий обзор линеаризованных уравнений движения для модели велосипеда Уиппла. Они использовали свои результаты для демонстрации самобалансирующегося велосипеда. Их исследование показывает, что этому явлению нельзя дать простое объяснение. Сочетание факторов, в том числе гироскопического и стабилизирующего эффектов, геометрии велосипеда, скорости и распределения массы позволяет неуправляемому велосипеду сохранять вертикальное положение.
Вдохновившись этой работой, мы построили динамическую модель многотельной системы, чтобы продемонстрировать самобалансирующееся движение велосипеда, управляемого велосипедистом без помощи рук.
Положение велосипеда в разные моменты времени.
Многотельная модель велосипеда
Чтобы обеспечить чистое качение колес и ограничить их проскальзывание в трех направлениях, нам нужны три граничных условия.
Модель колеса с отображением направлений, в которых ограничены перемещения.
Используются следующие ограничения: Отсутствие проскальзывания в прямом направлении:
{\frac{d\bold{u}}{dt}.\bold{e}_{2}=r\frac{d\bold{\theta}_s}{dt}}
Отсутствие проскальзывания в поперечном направлении:
\frac{d\bold{u}}{dt}.\bold{e}_{3}=r\frac{d\bold{\theta}_{l}}{dt}
Отсутствие проскальзывания перпендикулярно поверхности контакта с землей:
\frac{d\bold{u}}{dt}.\bold{e}_{4}=0
где \bold{e}_{2} , \bold{e}_{3} , and \bold{e}_{4} — мгновенное направление (наклонная ось), поперечное направление (ось вращения) и нормаль к поверхности контакта (\bold{e}_{4}=\bold{e}_{2} \times\bold{e}_{3}) , соответственно;
\frac{d\bold{u}}{dt} — поступательная скорость движения; r — радиус колеса; \frac{d\bold{\theta}_{s}}{dt} — угловая скорость вращения; \frac{d\bold{\theta}_{l}}{dt} — угловая наклонная скорость.
Поскольку применить указанные граничные условия к скорости невозможно, они дискретизируются во времени и накладываются следующим образом:
(\bold{u}-\bold{u}_{p}).\bold{e}_{2}=r(\bold{\theta}_{s}-\bold{\theta}_{sp})
(\bold{u}-\bold{u}_{p}).\bold{e}_{3}=r(\bold{\theta}_{l}-\bold{\theta}_{lp})
(\bold{u}-\bold{u}_{p}).\bold{e}_{4}=0
где \bold{u}_{p} , \bold{\theta}_{sp} и\bold{\theta}_{lp} — это вектор смещения, угол вращения и наклона в предыдущий момент времени, соответственно.
В дискретных граничных условиях, обеспечивающих отсутствие проскальзывания, используется результат расчета положения колеса на предыдущем шаге по времени. Положение жесткого тела, вращение и мгновенные положения осей на предыдущем шаге по времени сохраняются с помощью глобальных уравнений и узла Previous Solution в нестационарном решателе.
Моделирование движения самобалансирующегося велосипеда
Для анализа мы выбрали велосипед, угол наклона руля которого составляет 18°. Начальное значение скорости велосипеда составляет 4.6 м/с. Через 1 секунду после начала движения на велосипед в течение очень короткого периода времени воздействует сила 500 Н. Под действием силы велосипед отклоняется от прямолинейной траектории движения в заданном направлении.
В течении первой секунды велосипед движется вперед вдоль первоначально заданного направления с постоянной скоростью. Затем боковое усилие вызывает отклонение. Отметим, что велосипедист не держит руки на руле и не может управлять балансом велосипеда. Что происходит дальше? Мы можем заметить, что как только велосипед начинает наклоняться, руль поворачивается в направлении падения. Корректировка положения руля при падении приводит к восстановлению равновесия велосипеда.
Велосипед продолжает двигаться вперед, и в процессе движения начинает наклоняться в обратную сторону. Этот наклон меньше по величине, а движение руля точно следует за наклоном с небольшим отставанием. Такое колебание вправо-влево продолжается и в конечном итоге затухает. Велосипед движется вперед в строго вертикальном положении и слегка увеличивает скорость. Колебания руля, углы поворота и угловая скорость постепенно снижаются и затухают.
Движение велосипеда на ровной поверхности при отклонении от прямолинейного движения. Стрелка показывает наклон велосипеда.


Результаты расчета углов наклона и поворота руля (слева) и относительная угловая скорость (справа) велосипеда.
Проведение анализа устойчивости
Таким образом, мы узнали, что велосипед может самобалансироваться. Исследование показало, что невозможно выделить какой-то один параметр, определяющий устойчивость велосипеда. Конструкция велосипеда, распределение массы и скорость движения — все эти факторы влияют на устойчивость. Чтобы лучше понять это явление, мы провели дополнительный анализ для изучения влияния двух параметров — начальной скорости и наклона рулевой оси. Мы использовали описанную выше модель велосипеда с углом наклона оси руля 18° и начальной скоростью 4.6 м/с в качестве исходной конфигурации и провели параметрический анализ влияния этих двух факторов.
Различные значения начальной скорости
Велосипед не может оставаться в строго вертикальном положении, когда стоит на месте. Мы изменяли скорость движения от 2.6 м/с до 6.6 м/с с шагом 1 м/с, чтобы оценить влияние этого параметра. В диапазоне 2.6–3.6 м/с велосипед наклоняется слишком сильно и неустойчив. На скорости 5.6 м/с скорость наклона стремится к нулю, но сам угол наклона приобретает ненулевое значение. Хотя данная конфигурация устойчива, велосипед будет двигаться по кругу с небольшим наклоном. На 6.6 м/с наклон и угол поворота руля увеличиваются со временем, делая движение неустойчивым.
| Неустойчивое | Устойчивое | Неустойчивое | ||
|---|---|---|---|---|
| 2.6 м/с | 3.6 м/с | 4.6 м/с | 5.6 м/с | 6.6 м/с |


Устойчивый случай соответствует скорости 5.6 м/с (слева), а неустойчивый — скорости 6.6 м/с (справа).
Угол поворота руля
Узел рулевого управления очень важен для самобалансировки велосипеда. Если велосипедом невозможно управлять (например, если руль заклинило), то велосипед не сможет компенсировать наклон, поэтому он в итоге упадет. В этой связи, поворот оси руля, который контролирует уход вилки, также влияет на самобалансировку велосипеда.
Чтобы проанализировать влияние поворота оси руля на устойчивость велосипеда, мы изменяли углы поворота руля от 15° до 21° с шагом 1°. При угле в 15° наклон и угол поворота руля увеличиваются со временем, что делает данную конфигурацию неустойчивой. Велосипед устойчив в диапазоне от 16° до 19° и неустойчив для больших углов. При значениях поворота больше 19°, наклон и угол поворота колеблются, и эти осцилляции со временем возрастают, что приводит к потере устойчивости.
В этой публикации мы рассказали, как смоделировать движение неуправляемого самобалансирующегося велосипеда с помощью модуля Динамика многотельных систем (Multibody Dynamics) в COMSOL Multiphysics. Мы продемонстрировали, как реализовать ограничения на проскальзывание на жестком колесе через уравнения, а затем объединили эти ограничения с многотельной моделью велосипеда. Затем мы проанализировали влияние начальной скорости и поворота оси на устойчивость велосипеда. Оценив эти параметры, мы увидели, что велосипед может сохранять устойчивость в одной конфигурации и терять ее в другой.
Самобалансировка велосипеда является следствием целого ряда факторов. С помощью нашего анализа и в соответствии с предыдущими исследованиями мы продемонстрировали, что устойчивость велосипеда связана с его способностью "подруливать" в направлении наклона.
Продолжаем серию статей по автоматизации выполнения фигур пилотажа на малом ДПЛА. Настоящая статья имеет, прежде всего, образовательную цель: здесь мы покажем, как можно создать простейшую систему автоматического управления (САУ) на примере задачи выполнения фигуры пилотажа «бочка» при управлении летательным аппаратом только элеронами. Статья является второй в цикле публикаций «Пилотажный ДПЛА», рассказывающем о процессе постройки аппаратной и программной частей САУ в обучающей форме.
Введение
Итак, мы решили реализовать «бочку» в автоматическом режиме. Очевидно, что для автоматического выполнения фигуры необходимо сформулировать соответствующий закон управления. Процесс придумывания будет гораздо безболезненнее и быстрее, если использовать математическую модель движения ЛА. Проверка закона управления в лётном эксперименте хоть и возможна, но требует гораздо большего времени, к тому же может оказаться гораздо дороже в случае потери или повреждения аппарата.Так как при небольших углах атаки и скольжения самолёта его движение по крену практически не связано с движением в двух других каналах: путевом и продольном - для выполнения простой «бочки» достаточно будет построить модель движения только вокруг одной оси - оси ОХ связанной СК. По этой же причине, закон управления элеронами не будет существенно изменяться, когда дело дойдет до создания полной системы управления.
Модель движения
Уравнение движения ЛА вокруг продольной оси ОХ связанной СК крайне простое:Где - момент инерции относительно оси ОХ , а момент состоит из нескольких составляющих, из которых для реалистичного описания движения нашего самолёта достаточно рассмотреть только две:
Где - момент, обусловленный вращением ЛА вокруг оси ОХ (демпфирующий момент), - момент, обусловленный отклонением элеронов (управляющий момент). Последнее выражение записано в линеаризованной форме: момент крена линейно зависит от угловой скорости и угла отклонения элеронов с постоянными коэффициентами пропорциональности и соответственно.
Как известно (например, из Вики), линейному дифференциальному уравнению
Соответствует апериодическое звено первого порядка
Где - передаточная функция, - оператор дифференцирования, - постоянная времени, а - коэффициент усиления.
Как перейти от дифференциального уравнения к передаточной функции?
В нашем случае от параметров уравнения к параметрам передаточной функции можно перейти следующим образом (зная, что производная отрицательная):
Для апериодического звена постоянная времени равна времени, за которое выходная величина при единичном ступенчатом воздействии входной величины принимает значение, отличающееся от установившегося на величину ~5%, а коэффициент усиления численно равен установившемуся значению выходной величины при единичном ступенчатом воздействии:

В построенной модели движения есть два неизвестных параметра: коэффициент усиления и постоянная времени . Эти параметры выражаются через характеристики физической системы: момент инерции , а также производные момента крена и :
Таким образом, если известен момент инерции , то, определив параметры модели, по ним можно восстановить параметры системы.
Параметры модели. Момент инерции
Наш летательный аппарат состоит из следующих частей: крыло, фюзеляж с оперением, двигатель, аккумулятор (АКБ) и БРЭО:
К БРЭО относятся: плата автопилота, плата приёмника СНС, плата радиомодема, плата приёмника сигнала от управляющей аппаратуры, два регулятора напряжения, регулятор оборотов двигателя, а также соединительные провода.

В силу малого веса БРЭО, его вкладом в общий момент инерции можно пренебречь.
Как проводилась оценка величины момента инерции?
Оценку момента инерции можно провести следующим образом. Посмотрим на самолёт вдоль оси ОХ :

А затем представим его в виде следующей упрощённой модели:

Схема для расчёта момента инерции . Слева вверху - аккумулятор, справа внизу - двигатель. Двигатель и аккумулятор располагаются на оси фюзеляжа
Видно, что для создания модели были отброшены: киль, горизонтальное оперение, винт, а также БРЭО. При этом остались: фюзеляж, крыло, аккумулятор, двигатель. Измерив массы и характерные размеры каждой части, можно вычислить моменты инерции каждой части относительно продольной оси фюзеляжа:
Общее значение момента инерции ЛА относительно оси ОХ получим сложением моментов инерции частей:
Оценив вклад каждой из частей ЛА в общий момент инерции , получилось следующее:
- крыло - 96.3%,
- фюзеляж - 1.6 %,
- двигатель и аккумулятор - 2%,

Поэтому, несмотря на скромный вес (около 20% от общей взлётной массы ЛА), крыло имеет значительный момент инерции.
Параметры модели. Производные момента крена и
Вычисление производных момента крена – довольно трудная задача, связанная с расчётом аэродинамических характеристик ЛА численными методами или с помощью инженерных методик. Применение первых и вторых требует значительных временных, интеллектуальных и вычислительных затрат, которые оправданы при разработке систем управления большими самолётами, где стоимость ошибки всё же превышает затраты на построение хорошей модели. Для задачи управления БПЛА, масса которого не превосходит 2 кг, такой подход вряд ли оправдан. Другой способ вычисления этих производных - лётный эксперимент. Учитывая дешевизну нашего самолёта, а также близость подходящего поля для проведения такого эксперимента, для нас выбор был очевиден.Записав в автопилот прошивку для ручного управления и регистрации параметров, мы собрали самолёт и подготовили его к испытаниям:

В лётном эксперименте удалось получить данные по углу отклонения элеронов и угловой скорости вращения ЛА. Пилот управлял самолётом в ручном режиме, выполняя полёт по кругу, развороты и «бочки», а бортовое оборудование регистрировало и отправляло необходимую информацию на наземную станцию. В результате были получены необходимые зависимости: (град/с) и (б/р). Величина представляет собой нормированный угол отклонения элеронов: значение 1 соответствует максимальному отклонению, а значение −1 - минимальному:

Как теперь определить и из полученных данных? Ответ - измерить параметры переходного процесса по графикам и .
Как определялись коэффициенты k и T?
Коэффициент усиления определялся путём отнесения величины установившегося значения угловой скорости к величине отклонения элерона:

Зависимости угла отклонения элеронов и угловой скорости крена от времени, полученные в лётном эксперименте
На предыдущем рисунке участкам установившегося значения угловой скорости приблизительно соответствуют, например, отрезки вблизи моментов времени 422, 425 и 438 с (отмечены тёмно-красным на рисунке).
Постоянная времени определялась из тех же графиков. Для этого найдены участки резкого изменения угла отклонения элерона, а затем измерено время, за которое угловая скорость принимает значение, отличающееся от установившегося значения на 5%.
Результат определения значений постоянной времени и коэффициента усиления следующий: , . Этим значениям коэффициентов при известном значении момента инерции соответствуют следующие значения производных момента крена:
Верификация модели
Итак, построив модель, основой которой является апериодическое звеноМожно провести её верификацию, подав на вход сигнал , полученный из лётного эксперимента, и сравнить выходной сигнал модели с величиной , также полученной в эксперименте.
Как проводилось моделирование?
Инструмент для проведения моделирования мы выбирали, прежде всего, основываясь на возможности повторения результатов широким кругом читателей: это прежде всего означает, что программа должна быть в общественном доступе. В принципе задачу моделирования поведения апериодического звена первого порядка можно решить и создав свой собственный инструмент с нуля. Но так как в дальнейшем модель будет усложняться, то создание своего инструмента может отвлечь от основной задачи - создания САУ пилотажного ДПЛА. С учётом принципа открытости инструмента мы выбрали JSBsim .
В предыдущем разделе мы получили значения коэффициентов и . Используем их для моделирования движения самолета. Из прошлой статьи мы помним, что конфигурация модели самолета в JSBsim
задается при помощи XML
файла. Создадим собственную модель:
Так как мы строим модель движения аппарата только по крену, оставим многие из секций файла пустыми. В файле модели последовательно задаются следующие характеристики.
Геометрические размеры самолёта задаются в секции metrics : площадь крыла, размах, длина средней аэродинамической хорды, площадь горизонтального оперения, плечо горизонтального оперения, площадь вертикального оперения, плечо вертикального оперения, положение аэродинамического фокуса.
Массовые характеристики самолёта задаются в секции mass_balance : тензор инерции самолета, вес пустого самолета, положение центра масс.
Стоит отметить, что абсолютные положения аэродинамического фокуса и центра масс самолета не участвуют в расчете динамики аппарата, важно их относительное расположение.
Далее следуют секции, описывающие характеристики шасси самолета и его силовой установки.
В следующей секции, ответственной за систему управления , заполним канал, ответственный за управление по крену: укажем единственный вход fcs/aileron-cmd-norm , величина которого будет нормирована от -1 до 1.
Аэродинамические характеристики задаются в секции aerodynamics : силы задаются в скоростной системе координат, моменты - в связанной. Нас интересует момент по крену. В секции axis name=«ROLL» задаются функции, которые определяют момент сил от различных составляющих проекции момента аэродинамических сил на ось OX связанной системы координат. В нашей модели таких составляющих две. Первая составляющая - демпфирующий момент, который равен произведению угловой скорости на определенный ранее коэффициент . Вторая составляющая - это момент от элеронов при фиксированной скорости полёта: он равен произведению ранее определенного коэффициента на величину отклонения элеронов.
Стоит отметить, что при определении коэффициента была использована размерная величина . В наших полетных данные величина угловой скорости измерялась в градусах в секунду, тогда как в JSBSim используются радианы в секунду, поэтому коэффициент должен быть приведен к нужной нам размерности, т. е. разделен на 180 градусов и умножен на радиан. Записываем эти составляющие момента аэродинамических сил внутри функций произведения product . При моделировании результат выполнения всех функций суммируется и получается значение проекции аэродинамического момента на соответствующую ось.
Проверить созданную модель можно на экспериментальных данных, полученных при лётных испытаниях. Для этого создаем скрипт следующего содержания:
где точками обозначены пропущенные данные. В знакомом нам по предыдущей статье файле скрипта появился новый тип события («Time Notif»
), который позволяет задавать непрерывное изменение параметра по времени. Зависимость параметра от времени задана табличной функцией. JSBSim
линейно интерполирует значение функции между табличными данными. Процедура верификации модели движения по крену заключается в исполнении данного скрипта на созданной модели и сравнения результатов с экспериментальными.
Результат верификации показан на рисунке:

Как видно из рисунка, совпадение модели с реальностью чуть менее, чем полное.
Синтез управления для выполнения «бочки»
Получив модель, несложно определить, на какую величину и как долго необходимо отклонять элероны, чтобы выполнить «бочку». Одним из вариантов является следующий алгоритм отклонения:
Наличие отрезков длительностью по 0.1 с в начале и в конце алгоритма отклонения элеронов моделирует инертность сервопривода, который не может отклонить поверхности мгновенно. Модель показывает, что при таком законе отклонения элеронов ЛА должен выполнить один полный оборот вокруг оси ОХ , проверим?
Лётный эксперимент
Полученный закон управления элеронами был запрограммирован в автопилот, установленный на самолёт. Идея эксперимента проста: вывести самолёт в горизонтальный полёт, после чего задействовать полученный закон управления. В случае если реальное движение ЛА по крену соответствует созданной модели, то самолёт должен выполнить «бочку» - один полный оборот на 360 градусов.Отдельно выражаем благодарность нашему верному пилоту за труд, профессионализм и удобный багажник на приоре-универсал!
В процессе проведения эксперимента стало ясно, что модель движения по крену была построена удачно - самолёт выполнял одну «бочку» за другой, как только пилот задействовал запрограммированный закон управления. На следующем рисунке показана угловая скорость , записанная в процессе эксперимента, и полученная по результатам моделирования, а также угол крена и тангажа из лётного эксперимента:

А на следующем рисунке показаны зарегистрированные в лётном эксперименте сигналы на элероны, руль высоты (РВ) и руль направления (РН):

Вертикальными линиями обозначены моменты начала и окончания выполнения «бочки». Из рисунков видно, что в процессе выполнения «бочки» пилот не вмешивается в управление рулём высоты и рулём направления, также видно, что угол тангажа неизменно стремится уменьшиться при выполнении «бочки» - самолёт затягивает в пикирование, как это и было предсказано по результатам моделирования в авиасимуляторе (см. статью «Пилотажный ДПЛА. Как правильно сделать бочку»). Если внимательно рассмотреть предыдущие графики, то станет видно, что третья «бочка» даже не была закончена, потому что пилот вмешался в управление, чтобы вывести самолёт из пикирования: настолько сильно изменяется угол тангажа при выполнении «бочки» одними элеронами.
Замечания
Выводы
В результате проведённой работы мы показали один из способов создания модели движения ДПЛА по угловой скорости . В лётном эксперименте было доказано, что созданная модель движения вполне соответствует моделируемому объекту. На основании разработанной модели получен закон программного управления, позволяющий выполнять «бочку» в автоматическом режиме. Также мы убедились, что выполнить правильную «бочку» одними элеронами не получится, а также наглядно это продемонстрировали.Следующим этапом будет доработка закона управления путём добавления обратной связи, а также включение в управление руля высоты. Последнее потребует создание модели продольного движения нашего самолёта. По результатам работы выйдет следующая публикация.
Цели урока:
Обучающие (конечные результаты урока):
Знание: знать, что представляют собой процесс движения, как его организовать в Qbasic.
Понимание: уметь привести примеры движения, которые можно смоделировать на ЭВМ.
Применение: уметь составить программу, реализующую движение по заданной траектории, проверить ее на ЭВМ.
Анализ: уметь определить результаты работы строк из программы, выявить ошибки.
Синтез: уметь создать моделирующую программу с использованием движения.
Сравнительная оценка: сравнить между собой программы с использованием движения в графическом и текстовом режимах.
Развивающие: развитие общеучебных умений и навыков, воображения и фантазии.
Воспитательные: воспитание ученика самостоятельной, организованной личностью.
Оборудование:
компьютерный класс, язык программирования Qbasic, презентация по теме урока, проектор к ЭВМ, экран, карты урока, карточки с правильными ответами для самоконтроля, демонстрационные программы.
Ход урока:
Наш урок посвящен практическому применению операторов организации циклов. С их помощью мы научимся моделировать на компьютере процесс движения различных объектов.
Моделирование - это форма отражения действительности, а так как мы будем описывать движение на языке программирования, то полученные модели называют информационными.
Говоря о движении, сразу вспоминается крылатое выражение «Движение – это жизнь». И действительно, кто не хотел, чтобы неподвижная картинка на экране «ожила». Например, на ней пошел бы «настоящий» снег, неподвижный кораблик поплыл, а стрелки часов начали бы свой ход. Этому «волшебству» мы можем научиться сегодня на уроке.
Итак, вы узнаете,
Как смоделировать процесс движения по прямой;
Рассмотрите примеры программ;
Научитесь «оживлять» объекты;
Проанализируете готовые программы;
Сравните процесс движения в графическом и текстовом режимах.
Что такое движение? С физической точки зрения движение – это изменение положения тела с течением времени. Для начала мы будем моделировать движение простых объектов– точки, окружности, линий. Вспомним их форматы записи.
У каждого объекта выбирается точка с координатой (x,y), положение которой будет меняться. Если для окружности – это координата центра, то у линии (прямоугольника) - это только одна из точек.
Если мы хотим перемещать символы по экрану, то нам потребуются операторы: LOCATE для выбора положения символа и PRINT для его печати.
Каковы правила моделирования движения?
1) Выберем координаты.
2) Изобразим объект.
3) Сделаем паузу.
4) Сотрем объект (закрашивая его цветом фона, или на месте удаляемых символов будем печатать пробелы).
5) Выберем следующие координаты.
Хотелось бы обратиться к еще одному высказыванию О. Холмз: «В нашей жизни важно не столько положение, в котором мы находимся, сколько направление, в котором мы движемся». Помимо глубокого философского смысла, оно имеет самое прямое отношение к моделированию движения.
Для перемещения очень важно, по какой траектории будет двигаться объект: по прямой (в горизонтальном или вертикальном направлениям), или графикам различных функций. Сегодня мы уделим внимание только движению по прямой (в горизонтальном и вертикальном направлении).
Тренинг 1. Движение по горизонтали.
Определите по приведенным траекториям следующие данные и занесите в таблицу:
|
номер графика |
координата X меняется |
координата Y |
||
Тренинг 2. Движение по вертикали.
Определите по приведенным траекториям следующие данные и занесите в таблицу:
|
номер графика |
координата X |
координата Y меняется |
||
Составьте программу, моделирующую движение точки по траектории графика №_____.
Тренинг 3.
Определите по приведенным строкам программы направление, в котором движется объект (вверх, вниз, вправо или влево по экрану), обозначьте направление стрелками:
1) FOR Y= 5 TO 100 STEP 10 _____________________________
2) FOR X= 1 TO 400 STEP 1 _____________________________
3) FOR X= 300 TO 40 STEP -10 _____________________________
4) FOR Y= 200 TO 10 STEP -10 _____________________________
5) FOR Y= 105 TO 3 STEP 10 _____________________________
6) FOR X= а TO a-100 STEP -10_____________________________
Тренинг 4.
Определите результат выполнения программы:
CLS
SCREEN 12
FOR Y= 5 TO 25 STEP 1
X=10
LOCATE Y,X
PRINT “ *”
SLEEP 1
LOCATE Y,X
PRINT “ ”
NEXT Y
FOR Х= 10 TO 60 STEP 1
Y= 25
LOCATE Y,X
PRINT “ *”
SLEEP 1
LOCATE Y,X
PRINT “ ”
NEXT Х
END
Упражнения
- В предложенной программе внести следующие изменения:
- чтобы точка двигалась по заданной траектории из тренинга 1;
- чтобы точка двигалась по заданной траектории из тренинга 2;
- чтобы двигалась не точка, а окружность (радиус = 30);
- чтобы окружность двигалась в обратном направлении;
- чтобы двигался закрашенный прямоугольник со сторонами 50 и 30.
Подсказка. Форматы записи:
окружность CIRCLE (X, Y), R, C
закрашенный прямоугольник LINE (X,Y) – (X1,Y1), C, BF
Составить программу для моделирования движения символов по экрану, составляющих любое из предложенных слов:
Домашнее задание:
1) Смоделируйте на компьютере сюжет русской народной сказки «Колобок». Изобразите дорогу-лабиринт и колобка, который ее успешно преодолевает.
2) Действие одного из компьютерных вирусов на экране проявлялось тем, что напечатанные символы «ссыпались» вниз. Составьте программу, которая моделировала бы данный процесс.
3) Видоизмените программу, так, чтобы пользователь печатал слово в произвольном месте экрана, но его «постигала бы та же участь».
Подведение итогов урока.
Ответьте на вопросы:
1) Как организуется движение по горизонтальной траектории?
2) Как смоделировать движение по вертикали?
3) В чем отличие моделирования движения графических объектов и текстовых символов?
4) Какие процессы можно смоделировать, пользуясь полученными на уроке знаниями?
Моделирование движения заключается в искусственном воспроизведении процесса движения физическими или математическими методами, например, с помощью ЭВМ.
В качестве примеров физических методов моделирования могут быть названы исследования движения на различных макетах элементов дороги или полигонные испытания, где создаются искусственные условия, имитирующие реальное движение транспортных средств. Простейшим примером физического моделирования может служить распространенный метод проверки возможностей маневрирования и постановки на стоянку различных транспортных средств с помощью их моделей на заданной площади, изображенной в уменьшенном масштабе.
Наибольшее значение имеет математическое моделирование (вычислительный эксперимент), основывающееся на математическом описании транспортных потоков. Благодаря быстродействию ЭВМ, на которых осуществляется такое моделирование, удается в минимальное время провести исследование влияния многочисленных факторов на изменения различных параметров и их сочетания и получить данные для оптимизации управления движением (например, для регулирования на пересечении), которые невозможно обеспечить натурными исследованиями.
В основу вычислительного эксперимента с применением ЭВМ легло понятие модели объекта, то есть математическое описание, соответствующее данной конкретной системе и отражающее с требуемой точностью поведение ее в реальных условиях. Вычислительный эксперимент дешевле, проще натурного, легко управляем. Он открывает путь к решению больших комплексных проблем и оптимальному расчету транспортных систем, научно обоснованному планированию исследований. Недостаток вычислительного эксперимента состоит в том, что применимость его результатов ограничена рамками принятой математической модели, построенной на основе закономерностей, выявленных с помощью натурного эксперимента.
Изучение результатов натурного эксперимента позволяет получить функциональные соотношения и теоретические распределения, исходя из которых строится математическая модель. Математическое моделирование в вычислительном эксперименте целесообразно разделить на аналитическое и имитационное. Процессы функционирования систем при аналитическом моделировании описываются с помощью некоторых функциональных отношений или логических условий. Учитывая сложность процесса дорожного движения, для упрощения приходится прибегать к серьезным ограничениям. Однако, несмотря на это, аналитическая модель позволяет находить приближенное решение задачи. При невозможности получения решения аналитическим путем модель может исследоваться с применением численных методов, позволяющих находить результаты при конкретных начальных данных. В этом случае целесообразно использовать имитационное моделирование, подразумевающее применение ЭВМ и алгоритмическое описание процесса вместо аналитического.
Широкое применение имитационное моделирование может найти для оценки качества организации движения, а также при решении различных задач, связанных с проектированием автоматизированных систем управления дорожным движением, например, при решении вопроса об оптимальной структуре системы. К числу недостатков имитационного моделирования относят частный характер получаемых решений, а также большие затраты машинного времени для получения статически достоверного решения.
Следует отметить, что в настоящее время область моделирования транспортных потоков находится в стадии формирования. Различные аспекты моделирования исследуются в МАДИ, ВНИИБД, НИИАТ и других организациях.
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
РЕСПУБЛИКАНСКИЙ ИНСТИТУТ ИННОВАЦИОННЫХ ТЕХНОЛОГИЙ
КАФЕДРА ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Курсовая работа
Дисциплина «Математическое моделирование»
Тема: «Моделирование движения парашютиста»
Введение
1. Свободное падение тела с учетом сопротивления среды
2. Формулировка математической модели и ее описание.
3. Описание программы исследования с помощью пакета Simulink
4. Решение задачи программным путем
Список использованных источников
Введение
Формулировка проблемы :
Катапульта выбрасывает манекен человека с высоты 5000 метров. Парашют не раскрывается, манекен падает на землю. Оценить скорость падения в момент удара о землю. Оценить время достижения манекеном предельной скорости. Оценить высоту, на которой скорость достигла предельного значения. Построить соответствующие графики, провести анализ и сделать выводы.
Цель работы :
Научиться составлять математическую модель, решать дифференциальные уравнения программными средствами (используется язык технических вычислений MatLAB 7.0, пакет расширения Simulink) и анализировать полученные данные о математической модели.
1. Свободное падение тела с учетом сопротивления среды
При реальных физических движениях тел в газовой или жидкостной среде трение накладывает огромный отпечаток на характер движения. Каждый понимает, что предмет, сброшенный с большой высоты (например, парашютист, прыгнувший с самолета), вовсе не движется равноускоренно, так как по мере набора скорости возрастает сила сопротивления среды. Даже эту, относительно несложную, задачу нельзя решить средствами “школьной” физики: таких задач, представляющих практический интерес, очень много. Прежде чем приступать к обсуждению соответствующих моделей, вспомним, что известно о силе сопротивления.
Закономерности, обсуждаемые ниже, носят эмпирический характер и отнюдь не имеют столь строгой и четкой формулировки, как второй закон Ньютона. О силе сопротивления среды движущемуся телу известно, что она, вообще говоря, растет с ростом скорости (хотя это утверждение не является абсолютным). При относительно малых скоростях величина силы сопротивления пропорциональна скорости и имеет место соотношение, где определяется свойствами среды и формой тела. Например, для шарика - это формула Стокса, где - динамическая вязкость среды, r - радиус шарика. Так, для воздуха при t = 20°С и давлении 1 атм = 0,0182 H.c.м-2 для воды 1,002 H.c.м-2 , для глицерина 1480 H.c.м-2.
Оценим, при какой скорости для падающего вертикально шара сила сопротивления сравняется с силой тяжести (в движение станет равномерным).
![]() (1)
(1)
Пусть r= 0,1 м, = 0,8 кг/м (дерево). При падении в воздухе м/с, в воде 17 м/с, в глицерине 0,012 м/с.
На самом деле первые два результата совершенно не соответствуют действительности. Дело в том, что уже при гораздо меньших скоростях сила сопротивления становится пропорциональной квадрату скорости: . Разумеется, линейная по скорости часть силы сопротивления формально также сохранится, но если , то вкладом можно пренебречь (это конкретный пример ранжирования факторов). О величине k2 известно следующее: она пропорциональна площади сечения тела S, поперечного по отношению к потоку, и плотности среды и зависит от формы тела. Обычно представляют k2 = 0,5сS, где с - коэффициент лобового сопротивления - безразмерен. Некоторые значения с (для не очень больших скоростей) приведены на рис.1.
При достижении достаточно большой скорости, когда образующиеся за обтекаемым телом вихри газа или жидкости начинают интенсивно отрываться от тела, значение с в несколько раз уменьшается. Для шара оно становится приблизительно равным 0,1. Подробности можно найти в специальной литературе.
Вернемся к указанной выше оценке, исходя из квадратичной зависимости силы сопротивления от скорости.
для шарика
 (3)
(3)
Рис 1 . Значения коэффициента лобового сопротивления для некоторых тел, поперечное сечение которых имеет указанную на рисунке форму
Примем r = 0,1 м, =0,8.103 кг/м3 (дерево). Тогда для движения в воздухе (= 1,29 кг/м3) получаем 18 м/с, в воде(= 1.103 кг/м3) 0,65 м/с, в глицерине (= 1,26.103 кг/м3) 0,58 м/с.
Сравнивая с приведенными выше оценками линейной части силы сопротивления, видим, что для движения в воздухе и в воде ее квадратичная часть сделает движение равномерным задолго до того, как это могла бы сделать линейная часть, а для очень вязкого глицерина справедливо обратное утверждение. Рассмотрим свободное падение с учетом сопротивления среды. Математическая модель движения - уравнение второго закона Ньютона с учетом двух сил, действующих на тело: силы тяжести и силы сопротивления среды:
![]() (4)
(4)
Движение является одномерным; проецируя векторное уравнение на ось, направленную вертикально вниз, получаем
![]() (5)
(5)
Вопрос, который мы будем обсуждать на первом этапе, таков: каков характер изменения скорости со временем, если все параметры, входящие в уравнение (7) заданы? При такой постановке модель носит сугубо дескриптивный характер. Из соображений здравого смысла ясно, что при наличии сопротивления, растущего со скоростью, в какой-то момент сила сопротивления сравняется с силой тяжести, после чего скорость больше возрастать не будет. Начиная с этого момента, , и соответствующую установившуюся скорость можно найти из условия ![]() =0, решая не дифференциальное, а квадратное уравнение. Имеем
=0, решая не дифференциальное, а квадратное уравнение. Имеем
 (6)
(6)
(второй - отрицательный - корень, естественно, отбрасываем). Итак, характер движения качественно таков: скорость при падении возрастает от до . Как и по какому закону – это можно узнать, лишь решив дифференциальное уравнение (7).
Однако даже в столь простой задаче мы пришли к дифференциальному уравнению, которое не относится ни к одному из стандартных типов, выделяемых в учебниках по дифференциальным уравнениям, допускающих очевидным образом аналитическое решение. И хотя это не доказывает невозможность его аналитического решения путем хитроумных подстановок, но они не очевидны. Допустим, однако, что нам удастся найти такое решение, выраженное через суперпозицию нескольких алгебраических и трансцендентных функций – а как найти закон изменения во времени перемещения? Формальный ответ прост:
 (7)
(7)
но шансы на реализацию этой квадратуры уже совсем невелики. Дело в том, что класс привычных нам элементарных функций очень узок, и совершенно обычна ситуация, когда интеграл от суперпозиции элементарных функций не может быть выражен через элементарные функции в принципе. Математики давно расширили множество функций, с которыми можно работать почти так же просто, как с элементарными (т. е. находить значения, различные асимптотики, строить графики, дифференцировать, интегрировать). Тем, кто знаком с функциями Бесселя, Лежандра, интегральными функциями и еще двумя десятками других, так называемых специальных функций, легче находить аналитические решения задач моделирования, опирающихся на аппарат дифференциальных уравнений. Однако даже получение результата в виде формулы не снимает проблемы представления его в виде, максимально доступном для понимания, чувственного восприятия, ибо мало кто может, имея формулу, в которой сопряжены логарифмы, степени, корни, синусы и тем более специальные функции, детально представить себе описываемый ею процесс - а именно это есть цель моделирования.
В достижении этой цели компьютер - незаменимый помощник. Независимо от того, какой будет процедура получения решения - аналитической или численной, - задумаемся об удобных способах представления результатов. Разумеется, колонки чисел, которых проще всего добиться от компьютера (что при табулировании формулы, найденной аналитически, что в результате численного решения дифференциального уравнения), необходимы; следует лишь решить, в какой форме и размерах они удобны для восприятия. Слишком много чисел в колонке быть не должно, их трудно будет воспринимать, поэтому шаг, с которым заполняется таблица, вообще говоря, гораздо больше шага, с которым решается дифференциальное уравнение в случае численного интегрирования, т.е. далеко не все значения и , найденные компьютером, следует записывать в результирующую таблицу (табл. 2).
Таблица 2
Зависимость перемещения и скорости падения от времени (от 0 до 15 с)
| t(c) | S(m) | (м/с) | t(c) | S(m) | (м/с) |
Кроме таблицы необходимы графики зависимостей и ; по ним хорошо видно, как меняются со временем скорость и перемещение, т.е. приходит качественное понимание процесса.
Еще один элемент наглядности может внести изображение падающего тела через равные промежутки времени. Ясно, что при стабилизации скорости расстояния между изображениями станут равными. Можно прибегнуть и к цветовой раскраске - приему научной графики, описанному выше.
Наконец, можно запрограммировать звуковые сигналы, которые подаются через каждый фиксированный отрезок пути, пройденный телом - скажем, через каждый метр или каждые 100 метров - смотря по конкретным обстоятельствам. Надо выбрать интервал так, чтобы вначале сигналы были редкими, а потом, с ростом скорости, сигнал слышался все чаще, пока промежутки не сравняются. Таким образом, восприятию помогают элементы мультимедиа. Поле для фантазии здесь велико.
Приведем конкретный пример решения задачи о свободно падающем теле. Герой знаменитого фильма “Небесный тихоход” майор Булочкин, упав с высоты 6000 м в реку без парашюта, не только остался жив, но даже смог снова летать. Попробуем понять, возможно, ли такое на самом деле или же подобное случается только в кино. Учитывая сказанное выше о математическом характере задачи, выберем путь численного моделирования. Итак, математическая модель выражается системой дифференциальных уравнений.
 (8)
(8)
Разумеется, это не только абстрактное выражение обсуждаемой физической ситуации, но и сильно идеализированное, т.е. ранжирование факторов перед построением математической модели произведено. Обсудим, нельзя ли произвести дополнительное ранжирование уже в рамках самой математической модели с учетом конкретно решаемой задачи, а именно - будет ли влиять на полет парашютиста линейная часть силы сопротивления и стоит ли ее учитывать при моделировании.
Так как постановка задачи должна быть конкретной, мы примем соглашение, каким образом падает человек. Он опытный летчик и наверняка совершал раньше прыжки с парашютом, поэтому, стремясь уменьшить скорость, он падает не “солдатиком”, а лицом вниз, “лежа”, раскинув руки в стороны. Рост человека возьмем средний - 1,7 м, а полуобхват грудной клетки выберем в качестве характерного расстояния - это приблизительно 0,4 м. для оценки порядка величины линейной составляющей силы сопротивления воспользуемся формулой Стокса. Для оценки квадратичной составляющей силы сопротивления мы должны определиться со значениями коэффициента лобового сопротивления и площадью тела. Выберем в качестве коэффициента число с=1,2 как среднее между коэффициентами для диска и для полусферы (выбор дня качественной оценки правдоподобен). Оценим площадь: S = 1,7 ∙ 0,4 = 0,7(м2).
В физических задачах на движение фундаментальную роль играет второй закон Ньютона. Он гласит, что ускорение, с которым движется тело, прямо пропорционально действующей на него силе (если их несколько, то равнодействующей, т.е. векторной сумме сил) и обратно пропорционально его массе:
Так для свободно падающего тела под действием только собственной массы закон Ньютона примет вид:
Или в дифференциальном виде:
Взяв интеграл от этого выражения, получим зависимость скорости от времени:
Если в начальный момент V0 = 0, тогда .
![]()
 .
.
Выясним, при какой скорости сравняются линейная и квадратичная составляющие силы сопротивления. Обозначим эту скорость Тогда
![]()
Ясно, что практически с самого начала скорость падения майора Булочкина гораздо больше, и поэтому линейной составляющей силы сопротивления можно пренебречь, оставив лишь квадратичную составляющую.
После оценки всех параметров можно приступить к численному решению задачи. При этом следует воспользоваться любым из известных методов интегрирования систем обыкновенных дифференциальных уравнений: методом Эйлера, одним из методов группы Рунге - Кутта или одним из многочисленных неявных методов. Разумеется, у них разная устойчивость, эффективность и т.д. - эти сугубо математические проблемы здесь не обсуждаются.
Вычисления производятся до тех пор, пока не опустится на воду. Примерно через 15 с после начала полета скорость становится постоянной и остается такой до приземления. Отметим, что в рассматриваемой ситуации сопротивление воздуха радикально меняет характер движения. При отказе от его учета график скорости, изображенный на рисунке 2, заменился бы касательной к нему в начале координат.

Рис. 2. График зависимости скорости падения от времени
2. Формулировка математической модели и ее описание
парашютист падение сопротивление математическая модель
При построении математической модели необходимо соблюдение следующих условий:
Манекен массой 50 кг соответственно падают в воздухе с плотностью 1,225 кг/м3;
На движение влияют только силы линейного и квадратичного сопротивления;
Площадь сечения тела S=0.4 м2;
Тогда для свободно падающего тела под действием сил сопротивления закон Ньютона примет вид:
![]() ,
,
где a – ускорение тела, м/с2,
m – его масса, кг,
g – ускорение свободного падения на земле, g = 9,8 м/с2,
v – скорость тела, м/c,
k1 – линейный коэффициент пропорциональности, примем k1 = β = 6πμl (μ – динамическая вязкость среды, для воздуха μ = 0,0182 Н.с.м-2; l – эффективная длина, примем для среднестатистического человека при росте 1,7 м и соответствующем обхвате грудной клетки l = 0,4 м),
k2 – квадратичный коэффициент пропорциональности. K2 = α = С2ρS. В данном случае достоверно можно узнать лишь плотность воздуха, а площадь манекена S и коэффициент лобового сопротивления С2 для него определить сложно, можно воспользоваться полученными экспериментальными данными и принять K2 = α = 0,2.
Тогда получим закон Ньютона в дифференциальном виде:


Тогда можно составить систему дифференциальных уравнений:

Математическая модель при падении тела в гравитационном поле с учетом сопротивления воздуха выражается системой из двух дифференциальных уравнений первого порядка.
3. Описание программы исследования с помощью пакета Simulink
Для имитационного моделирования движения парашютиста в системе MATLAB используем элементы пакета расширения Simulink. Для задания величин начальной высоты - H_n, конечной высоты - H_ k, числа - pi, μ – динамическая вязкость среды - my, обхват - R, массе манекена m, коэффициент лобового сопротивления - c, плотность воздуха - ro, площадь сечения тела - S, ускорение свободного падения - g, начальная скорость - V_n используем элемент Constantнаходящийся в Simulink/Sources(рисунок 3).

Рисунок 3. Элемент Constant
Для операции умножения используем блок Product, находящийся в Simulink/MathOperations/Product (рисунок 4).
Рисунок. 4
Для ввода k1 – линейного коэффициента пропорциональности и k2 – квадратичного коэффициента пропорциональности используем элемент Gain, находящийся в Simulink/MathOperations/Gain(Рисунок. 5.)
![]()
Рисунок. 5
Для интегрирования – элемент Integrator. Находящийсяв Simulink/Continuous/Integrator. Рисунок. 6.
![]()
Рисунок. 6
Для вывода информации используем элементы Display и Scope. Находящиеся в Simulink/Sinks. (Рисунок. 7)

Рисунок. 7
Математическая модель для исследования с использованием вышеперечисленных элементов, описывающая последовательный колебательный контур приведена на рисунке 8.

Рисунок. 8
Программа исследований
1. Исследование графика зависимости высоты от времени и скорости от времени масса парашютиста равна 50кг.

Рисунок 9
Из графиков видно, что при расчете падения парашютиста массой 50 кг, следующие данные: максимальная скорость равна 41,6 м/с и время равно 18с, и должна достигаться через 800 м падения, т.е. в нашем случае на высоте около 4200 м.

Рисунок. 10
2. Исследование графика зависимости высоты от времени и скорости от времени масса парашютиста равна 100кг.

Рисунок 11

Рисунок 12
С массой парашютиста 100 кг.: максимальная скорость равна 58 м/с и время равно 15с, и должна достигаться через 500 м падения, т.е. в нашем случае на высоте около 4500 м. (рисунок. 11., рисунок. 12).
Выводы по полученным данным, которые справедливы для манекенов, отличающихся только массой, но с одинаковыми размерами, формой, типом поверхности и другими параметрами, определяющими внешний вид объекта.
Легкий манекен при свободном падении в гравитационном поле с учетом сопротивления среды достигает меньшей предельной скорости, но за меньший промежуток времени и, естественно, при одинаковой начальной высоте – в более низкой точке траектории, чем тяжелый манекен.
Чем тяжелее манекен, тем быстрее он достигнет земли.
4. Решение задачи программным путем
%Функция моделирования движения парашютиста
function dhdt=parashut(t,h)
global k1 k2 g m
% система ДУ первого порядка
dhdt(1,1)= -h(2);
% Моделирование движения парашютиста
% Васильцов С. В.
global h0 g m k1 k2 a
% k1-линейный коэффициент пропорциональности, определяющийся свойствами среды и формой тела. Формула Стокса.
k1=6*0.0182*0.4;
%k2-квадратичный коэффициент пропорциональности, пропорционален площади сечения тела, поперечного по
%отношения к потоку, плотности среды и зависит от формы тела.
k2=0.5*1.2*0.4*1.225
g=9.81; % ускорение свободного падения
m=50; % масса манекена
h0=5000; % высота
Ode45(@parashut,,)
r=find(h(:,1)>=0);
a=g-(k1*-h(:,2)+k2*h(:,2).*h(:,2))/m % вычисляемускорение
% Построение графика зависимости высоты от времени
subplot(3,1,1), plot(t,h(:,1),"LineWidth",1,"Color","r"),grid on;
xlabel("t, c"); ylabel("h(t), m");
title("Графикзависимостивысотыотвремени", "FontName", "Arial","Color","r","FontWeight","bold");
legend("m=50 kg")
% Построение графика зависимости скорости от времени
subplot(3,1,2), plot(t,h(:,2),"LineWidth",1,"Color","b"),grid on;
ylabel("V(t), m/c");
Title("Графикзависимостискоростиотвремени", "FontName", "Arial","Color","b","FontWeight","bold");
legend("m=50 kg")
% Построение графика зависимости ускорения от времени
subplot(3,1,3), plot(t,a,"-","LineWidth",1,"Color","g"),grid on;
text (145, 0,"t, c");
ylabel("a(t), m/c^2");
Title("Графикзависимостиускоренияотвремени", "FontName", "Arial","Color","g","FontWeight","bold");
legend("m=50 kg")
Экранная форма вывода графиков.





1. Вся физика. Е.Н. Изергина. – М.: ООО «Издательство «Олимп», 2001. – 496 с.
2. Касаткин И. Л. Репетитор по физике. Механика. Молекулярная физика. Термодинамика/ Под ред. Т. В. Шкиль. – Ростов Н/Д: изд-во «Феникс», 2000. – 896 с.
3. Компакт-диск «Самоучитель MathLAB». ООО «Мультисофт», Россия, 2005.
4. Методические указания к Курсовой работе: дисциплина Математическое моделирование. Движение тела при учете сопротивления среды. – Минск. РИИТ БНТУ. Кафедра ИТ, 2007. – 4 с.
5. Решение систем дифференциальных уравнений в Matlab. Дубанов А.А. [Электронный ресурс]. – Режим доступа: http://rrc.dgu.ru/res/exponenta/ educat/systemat/dubanov/index.asp.htm;
6. Энциклопедия д.д. Физика. Т. 16. Ч.1. с. 394 – 396. Сопротивление движению и силы трения. А. Гордеев. /Глав. ред. В.А. Володин. – М. Аванта+, 2000. – 448 с.
7. MatlabFunctionReference [Электронный ресурс]. – Режим доступа: http://matlab.nsu.ru/Library/Books/Math/MATLAB/help/techdoc/ref/.